# Load required packages
library(dplyr) # For data manipulation
library(ggplot2) # For visualization
library(gganimate) # For animations
library(metR) # For geom_arrowImplementing Particle Swarm Optimization from Scratch in R
Introduction
Nature-inspired optimization algorithms demonstrate remarkable efficiency in solving complex optimization problems. This post provides a implementation of Particle Swarm Optimization (PSO) from fundamental principles in R. The methodology presented enables efficient exploration of complex solution spaces through coordinated swarm intelligence.
Package Dependencies
Optimization Test Function: Ackley’s Function
This tutorial employs Ackley’s function as the optimization benchmark—a challenging multimodal function characterized by numerous local minima that frequently entrap conventional optimization algorithms:
obj_func <- function(x, y){
# Modified Ackley function with global minimum at (1,1)
-20 * exp(-0.2 * sqrt(0.5 *((x-1)^2 + (y-1)^2))) -
exp(0.5*(cos(2*pi*x) + cos(2*pi*y))) + exp(1) + 20
}
# Create a visualization grid
x <- seq(-5, 5, length.out = 50)
y <- seq(-5, 5, length.out = 50)
grid <- expand.grid(x, y, stringsAsFactors = FALSE)
grid$z <- obj_func(grid[,1], grid[,2])
# Create a contour plot
contour_plot <- ggplot(grid, aes(x = Var1, y = Var2)) +
geom_contour_filled(aes(z = z), color = "black", alpha = 0.5) +
scale_fill_brewer(palette = "Spectral") +
theme_minimal() +
labs(x = "x", y = "y", title = "Ackley's Function")
contour_plot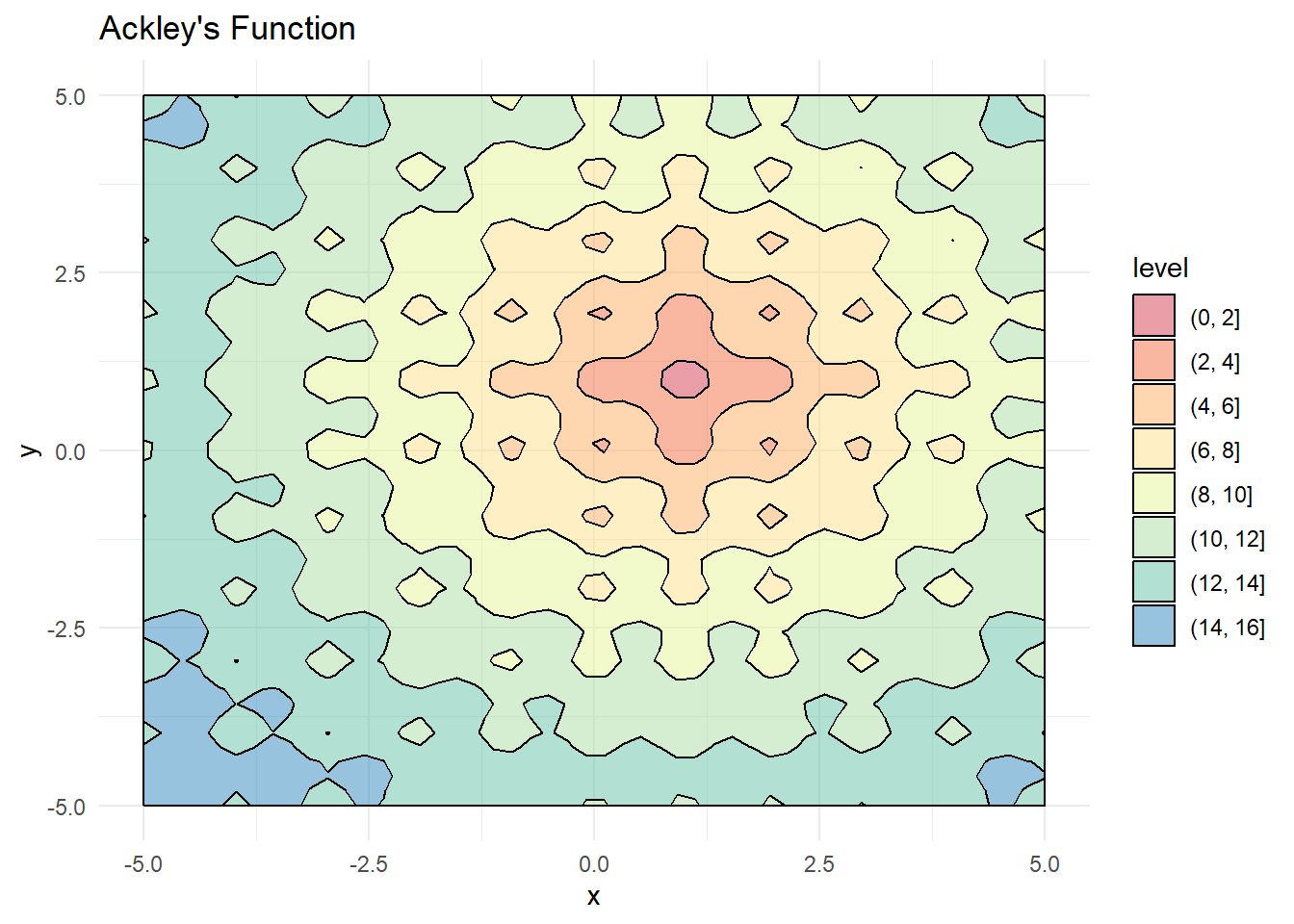
Theoretical Foundation of Particle Swarm Optimization
PSO emulates the collective foraging behavior of biological swarms through the integration of individual memory with social information sharing:
- Initialization: Random distribution of particles across the search space
- Memory Mechanism: Each particle maintains a record of its personal best position
- Information Sharing: The swarm collectively maintains knowledge of the global best position
- Movement Dynamics: Particles adjust their trajectories based on both personal experience and collective knowledge
The velocity update equation represents a balance of three fundamental forces:
\[v_{new} = w \cdot v_{current} + c_1 \cdot r_1 \cdot (p_{best} - p_{current}) + c_2 \cdot r_2 \cdot (g_{best} - p_{current})\]
Where:
w: Inertia (momentum preservation)c1: Personal influence (individual memory)c2: Social influence (collective cooperation)r1,r2: Stochastic components
Sample Implementation
Swarm Initialization
The initial phase involves creating a randomized swarm of particles and distributing them across the defined search space:
# Set parameters
n_particles <- 20
w <- 0.5 # Inertia weight
c1 <- 0.05 # Personal learning rate
c2 <- 0.1 # Social learning rate
# Create random particle positions
x_range <- seq(-5, 5, length.out = 20)
y_range <- seq(-5, 5, length.out = 20)
X <- data.frame(
x = sample(x_range, n_particles, replace = FALSE),
y = sample(y_range, n_particles, replace = FALSE)
)
# Visualize initial positions
contour_plot +
geom_point(data = X, aes(x, y), color = "red", size = 2.5) +
labs(title = "Initial Particle Positions")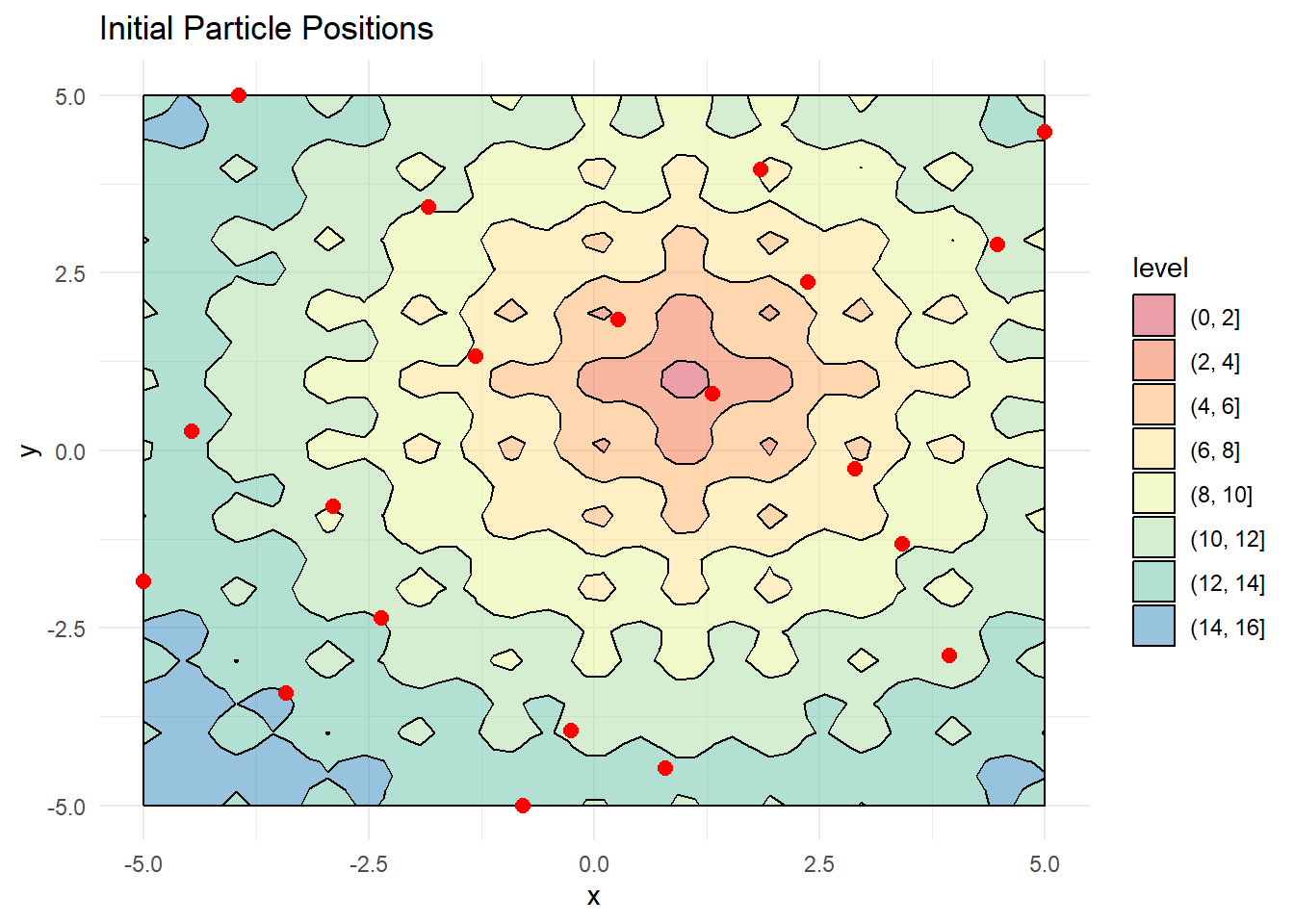
Global Best Position and Velocity Initialization
Next, we need to track each particle’s personal best position and the swarm’s global best position, while initializing velocity vectors:
# Initialize random velocities
dX <- matrix(runif(n_particles * 2), ncol = 2) * w
# Set initial personal best positions
pbest <- X
pbest_obj <- obj_func(X[,1], X[,2])
# Find global best position
gbest <- pbest[which.min(pbest_obj),]
gbest_obj <- min(pbest_obj)
# Visualize with arrows showing pull toward global best
X_dir <- X %>%
mutate(g_x = gbest[1,1],
g_y = gbest[1,2],
angle = atan((g_y - y)/(g_x - x))*180/pi,
angle = ifelse(g_x < x, 180 + angle, angle))
contour_plot +
geom_point(data = X, aes(x, y), color = "red", size = 2.5) +
geom_segment(data = X_dir,
aes(x = x, y = y,
xend = x + 0.5*cos(angle*pi/180),
yend = y + 0.5*sin(angle*pi/180)),
arrow = arrow(length = unit(0.1, "cm")),
color = "blue") + labs(title = "Forces Acting on Particles")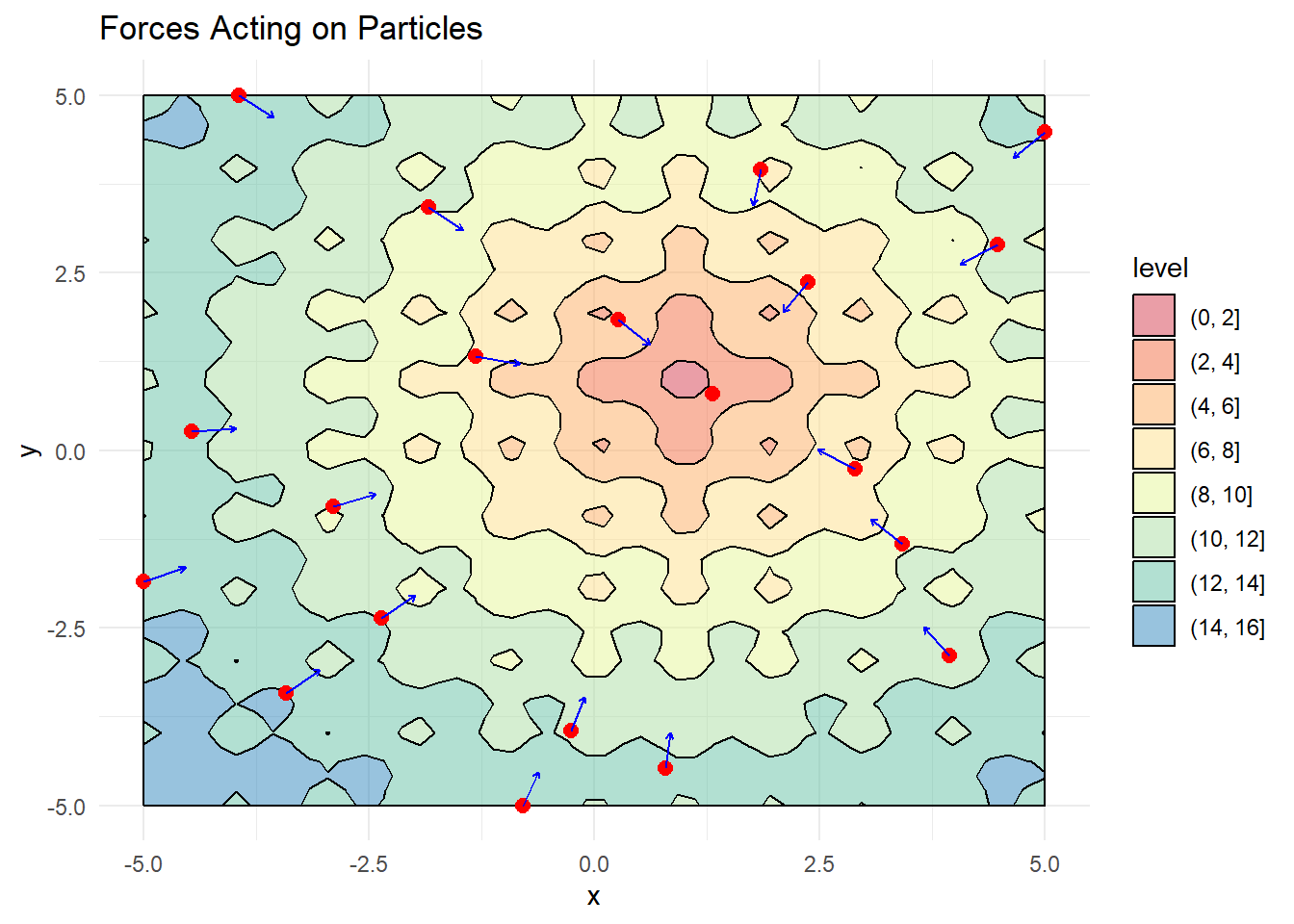
Position Update Mechanism
The position update process implements the core PSO algorithm, calculating new velocities based on the fundamental equation and updating particle positions accordingly:
# Calculate new velocities using PSO equation
dX <- w * dX +
c1*runif(1)*(pbest - X) +
c2*runif(1)*(as.matrix(gbest) - X)
# Update positions
X <- X + dX
# Evaluate function at new positions
obj <- obj_func(X[,1], X[,2])
# Update personal best positions if improved
idx <- which(obj <= pbest_obj)
pbest[idx,] <- X[idx,]
pbest_obj[idx] <- obj[idx]
# Update global best position
idx <- which.min(pbest_obj)
gbest <- pbest[idx,]
gbest_obj <- min(pbest_obj)
# Visualize updated positions
X_dir <- X %>%
mutate(g_x = gbest[1,1],
g_y = gbest[1,2],
angle = atan((g_y - y)/(g_x - x))*180/pi,
angle = ifelse(g_x < x, 180 + angle, angle))
contour_plot +
geom_point(data = X, aes(x, y), color = "red", size = 2.5) +
geom_segment(data = X_dir,
aes(x = x, y = y,
xend = x + 0.5*cos(angle*pi/180),
yend = y + 0.5*sin(angle*pi/180)),
arrow = arrow(length = unit(0.1, "cm")),
color = "blue") +
labs(title = "Particles After First Update")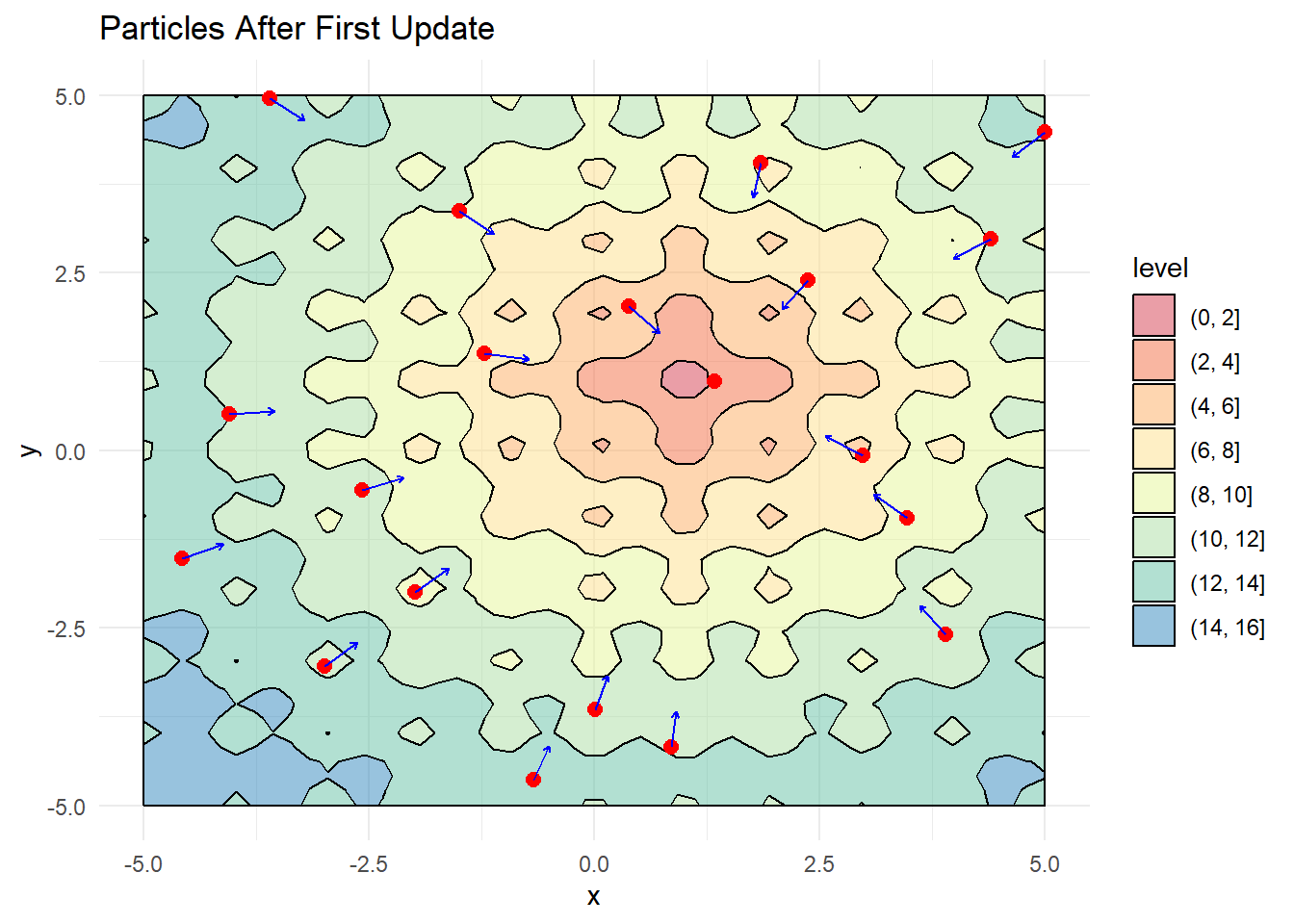
Full Implementation
The following implementation encapsulates the complete PSO algorithm within a reusable function framework:
pso_optim <- function(obj_func, # Function to minimize
c1 = 0.05, # Personal learning rate
c2 = 0.05, # Social learning rate
w = 0.8, # Inertia weight
n_particles = 20, # Swarm size
init_fact = 0.1, # Initial velocity factor
n_iter = 50 # Maximum iterations
){
# Define search domain
x <- seq(-5, 5, length.out = 100)
y <- seq(-5, 5, length.out = 100)
# Initialize particles
X <- cbind(sample(x, n_particles, replace = FALSE),
sample(y, n_particles, replace = FALSE))
dX <- matrix(runif(n_particles * 2) * init_fact, ncol = 2)
# Initialize best positions
pbest <- X
pbest_obj <- obj_func(x = X[,1], y = X[,2])
gbest <- pbest[which.min(pbest_obj),]
gbest_obj <- min(pbest_obj)
# Store positions for visualization
loc_df <- data.frame(X, iter = 0)
iter <- 1
# Main optimization loop
while(iter < n_iter){
# Update velocities
dX <- w * dX +
c1*runif(1)*(pbest - X) +
c2*runif(1)*t(gbest - t(X))
# Update positions
X <- X + dX
# Evaluate and update best positions
obj <- obj_func(x = X[,1], y = X[,2])
idx <- which(obj <= pbest_obj)
pbest[idx,] <- X[idx,]
pbest_obj[idx] <- obj[idx]
# Update global best
idx <- which.min(pbest_obj)
gbest <- pbest[idx,]
gbest_obj <- min(pbest_obj)
# Store for visualization
iter <- iter + 1
loc_df <- rbind(loc_df, data.frame(X, iter = iter))
}
return(list(X = loc_df,
obj = gbest_obj,
obj_loc = paste0(gbest, collapse = ",")))
}The following code snippet applies the PSO algorithm to the Ackley function:
# Run the PSO algorithm
out <- pso_optim(obj_func,
c1 = 0.01, # Low personal influence
c2 = 0.05, # Moderate social influence
w = 0.5, # Medium inertia
n_particles = 50,
init_fact = 0.1,
n_iter = 200)
# Check the result (global minimum should be at (1,1))
out$obj_loc[1] "1.00001492144968,1.00002681289027"Visualising Swarm Behavior
The optimization process can be effectively visualized through animation, demonstrating the collective convergence behavior of the particle swarm:
# Create animation of the optimization process
ggplot(out$X) +
geom_contour(data = grid, aes(x = Var1, y = Var2, z = z), color = "black") +
geom_point(aes(X1, X2)) +
labs(x = "X", y = "Y") +
transition_time(iter) +
ease_aes("linear")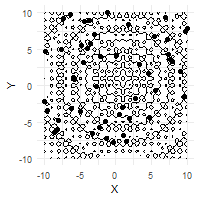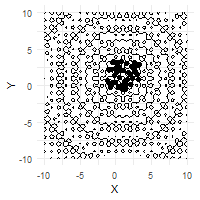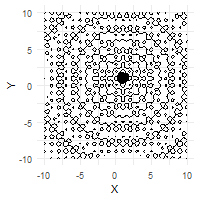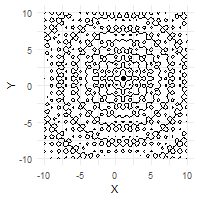
Parameter Optimization and Algorithm Tuning
The PSO algorithm’s performance characteristics can be substantially modified through systematic adjustment of three parameters:
- Inertia Weight (w)
- High values (>0.8): Particles maintain substantial momentum, aiding extensive exploration
- Low values (<0.4): Particles exhibit reduced momentum, facilitating solution refinement
- Personal Learning Rate (c1)
- High values: Particles prioritize individual discoveries and historical performance
- Low values: Particles demonstrate reduced reliance on personal experience
- Social Learning Rate (c2)
- High values: Particles demonstrate strong attraction toward the global optimum
- Low values: Particles maintain greater independence in exploration
Implementation Considerations
- Boundary Constraint Implementation: Enforce particle confinement within valid solution regions
- Adaptive Parameter Strategies: Implement dynamic parameter adjustment during optimization execution
- Convergence-Based Termination: Establish sophisticated stopping criteria based on solution convergence
- High-Dimensional Extension: Adapt the algorithm for complex, multi-dimensional optimization problems
The R package
psoprovides a comprehensive, production-ready implementation suitable for industrial applications.
Key Takeaways
- PSO successfully emulates biological swarm intelligence through mathematical modeling of collective behavior patterns
- The velocity update equation balances three critical forces: inertia, personal experience, and social influence
- Parameter tuning significantly affects algorithm performance, with distinct configurations optimizing exploration versus exploitation
- The algorithm scales effectively to high-dimensional problems while maintaining computational efficiency
- Production implementations require boundary constraints and adaptive parameters for robust performance